加密算法
导语
本文尝试由古及今,论述加密算法的发展演变,以及在整个过程中先后出现的几种关键加密算法及其优劣势对比。由于个人水平有限,如果出现谬误,还望不吝赐教。
签名算法和加密算法
签名算法
也叫杂凑函数、散列函数或哈希函数,可将任意长度的消息经过运算,变成固定长度数值,常见的有MD5、SHA-1、SHA256,多应用在文件校验,数字签名中。
| 算法 | 输出长度(位) | 输出长度(字节) |
|---|---|---|
| MD5 | 128 bits | 16 bytes |
| SHA-1 | 160 bits | 20 bytes |
| RipeMD-160 | 160 bits | 20 bytes |
| SHA-256 | 256 bits | 32 bytes |
| SHA-512 | 512 bits | 64 bytes |
根据碰撞概率,哈希算法的输出长度越长,就越难产生碰撞,也就越安全。
签名算法是一个不可逆过程,就是无论多大数据,经过算法运算后都是生成固定长度的数据,一般结果使用16进制进行显示。
主要用途有:验证消息完整性,安全访问认证,数据签名。
消息完整性:由于每一份数据生成的MD5值不一样,因此发送数据时可以将数据和其MD5值一起发送,然后就可以用MD5验证数据是否丢失、修改。在下文中对数据内容的完整性就是通过比较发送内容的MD5和接收到的内容的MD5是否一样判断其完整性。
安全访问认证:这是使用了算法的不可逆性质,(就是无法从MD5值中恢复原数据)对账号登陆的密码进行MD5运算然后保存,这样可以保证除了用户之外,即使数据库管理人员都无法得知用户的密码。
数字签名:这是结合非对称加密算法和CA证书的一种使用场景。
一般破解方法:字典法,就是将常用密码生成MD5值字典,然后反向查找达到破解目的,因此建议使用强密码
加密算法
加密算法主要作用是把明文变成密文。加密算法加密后,明文会变成密文,防止信息泄露。虽然看起来和乱码很像,但密文不是乱码。
加密算法的采用需要符合以下三点诉求:
机密性:
消息的发送方能够确定消息只有预期的接收方可以解密(不保证第三方无法获得,但保证第三方无法解密)。
完整性:
消息的接收方可以确定消息在途中没有被篡改过
可用性:
保证加密算法的开销、复杂度都在可用范围。
大部分乱码是由于编码不一致导致。编码不属于加密算法,编码无法把明文变成密文,只是改变了一种显示格式而已。所以base64只是一种编码而已,它不是加密算法,不具备加密能力,不能保障您的明文安全。所以,以后要听哪家说我们使用了base64进行加密,赶紧屏蔽。
结合上述诉求,加密算法的发展主要经历了古典密码、近代密码和现代密码三个重要时期。
密码学
密码学是网络安全、信息安全、区块链等产品的基础,常见的非对称加密、对称加密、散列函数等,都属于密码学范畴。
密码学有数千年的历史,从最开始的替换法到如今的非对称加密算法,经历了古典密码学,近代密码学和现代密码学三个阶段。密码学不仅仅是数学家们的智慧,更是如今网络空间安全的重要基础。
古典密码学
在古代的战争中,多见使用隐藏信息的方式保护重要的通信资料。比如先把需要保护的信息用化学药水写到纸上,药水干后,纸上看不出任何的信息,需要使用另外的化学药水涂抹后才可以阅读纸上的信息。
再比如把需要保护的信息写到送信人的头皮上,等头发长出来后,把送信人送达目的地,再剃光头发阅读信息。
这些方法都是在保护重要的信息不被他人获取,但藏信息的方式比较容易被他人识破,例如增加哨兵的排查力度,就会发现其中的猫腻,因而随后发展出了较难破解的古典密码学。
替换法
替换法很好理解,就是用固定的信息将原文替换成无法直接阅读的密文信息。例如将b替换成w,e替换成p,这样bee单词就变换成了wpp,不知道替换规则的人就无法阅读出原文的含义。
替换法有单表替换和多表替换两种形式。单表替换即只有一张原文密文对照表单,发送者和接收者用这张表单来加密解密。在上述例子中,表单即为:abcde-swtrp。
多表替换即有多张原文密文对照表单,不同字母可以用不同表单的内容替换。
例如约定好表单为:表单1:abcde-swtrp、表单2:abcde-chfhk、表单3:abcde-jftou。
规定第一个字母用第三张表单,第二个字母用第一张表单,第三个字母用第二张表单,这时bee单词就变成了(312)fpk,破解难度更高,其中312又叫做密钥,密钥可以事先约定好,也可以在传输过程中标记出来。
移位法
移位法就是将原文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后得出密文,典型的移位法应用有“恺撒密码”。
例如约定好向后移动2位(abcde-cdefg),这样bee单词就变换成了dgg。
同理替换法,移位法也可以采用多表移位的方式,典型的多表案例是“维尼吉亚密码”(又译维热纳尔密码),属于多表密码的一种形式。
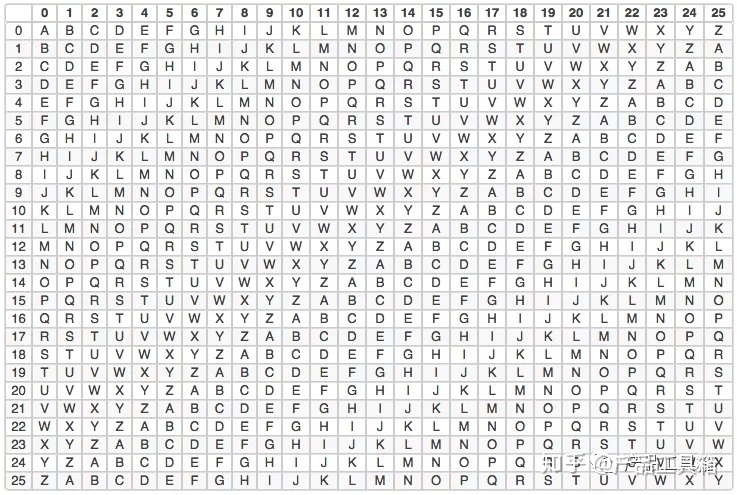
古典密码破解方式
古典密码虽然很简单,但是在密码史上是使用的最久的加密方式,直到“概率论”的数学方法被发现,古典密码就被破解了。
英文单词中字母出现的频率是不同的,e以12.702%的百分比占比最高,z只占到0.074%,感兴趣的可以去百科查字母频率详细统计数据。如果密文数量足够大,仅仅采用频度分析法就可以破解单表的替换法或移位法。
多表的替换法或移位法虽然难度高一些,但如果数据量足够大的话,也是可以破解的。以维尼吉亚密码算法为例,破解方法就是先找出密文中完全相同的字母串,猜测密钥长度,得到密钥长度后再把同组的密文放在一起,使用频率分析法破解。
古代人民如何加密?
1. 历史上最早的加密算法
早期加密算法主要使用在军事中,历史上最早关于加密算法的记载出自于周朝兵书《六韬.龙韬》中的《阴符》和《阴书》。其中记载:
太公曰:“主与将,有阴符,凡八等。有大胜克敌之符,长一尺。破军擒将之符,长九寸。降城得邑之符,长八寸。却敌报远之符,长七寸。警众坚守之符,长六寸。请粮益兵之符,长五寸。败军亡将之符,长四寸。失利亡士之符,长三寸。诸奉使行符,稽留,若符事闻,泄告者,皆诛之。八符者,主将秘闻,所以阴通言语,不泄中外相知之术。敌虽圣智,莫之能识。”
武王问太公曰:“… 符不能明;相去辽远,言语不通。为之奈何?” 太公曰:“诸有阴事大虑,当用书,不用符。主以书遗将,将以书问主。书皆一合而再离,三发而一知。再离者,分书为三部。三发而一知者,言三人,人操一分,相参而不相知情也。此谓阴书。敌虽圣智,莫之能识。”
简单来说,阴符是以八等长度的符来表达不同的消息和指令,属于密码学中的替代法,在应用中是把信息转变成敌人看不懂的符号,但知情者知道这些符号代表的含义。这种符号法无法表达丰富的含义,只能表述最关键的八种含义。阴书作为阴符的补充,运用了文字拆分法直接把一份文字拆成三分,由三种渠道发送到目标方手中。敌人只有同时截获三分内容才可能破解阴书上写的内容。
上述朴素的加密算法思想主要使用了替换法。无独有偶,在遥远的西方加密算法也大规模使用于战争之中。在希罗多德(Herodotus)的《历史》中记载了公元前五世纪,希腊城邦和波斯帝国发生多次冲突和战争。这些战争中希腊城邦中广泛使用了移位法进行加密处理战争通讯信息,使波斯帝国难以获得希腊城邦的军事情报,也就无法提前做军事部署。
希腊城邦用来传输军事信息、命令的每段文字都有固定的字数,解密者手中会有一份文字移位说明。解密者拿到密文后,根据文字移位说明进行解密,从而破解其中的军事命令或消息。
2. 古代密码演变的凯撒密码
古典密码主要采用的就是移动法和替换法。经过逐渐发展和完善,最有名的莫过于凯撒密码。凯撒密码有两种模式——移位法和替换法。其中,移位法就是让明文都向固定方向移动特定位数,例如I love you右移动4位就变成了M pszi csy。但英文或拉丁文,字母出现的频率并不一致。以英文字母为例:字母e出现频率明显高过其他字母。在获得足够多的密文样本后,可以通过频率计算准确找到移位规则,从而破解密文。同时由于需要可逆操作,所以实际上密钥的数量是有限的,只有25种可能。因此,完全可以通过暴力破解来对密文进行解密。
于是大部分凯撒密码在实际应用中都采用了第二种模式——替换法。定义一张明文密文映射表:

这种方式可以在一定程度上解决密钥可穷举的问题,但仍对大数据量的频率攻击束手无策。后来,这种模式发展为,靠引入一些特定参数来扰乱频率,这在一定程度上提高了解密的难度,但仍属于替换法和移位法的范畴。
古典密码后期发展出维吉尼亚密码、ROT5/13/18/47、摩尔斯密码等一系列密码种类。但都是以替换法和移位法为核心基础,安全性也主要是靠算法不公开来保证。所使用的加密算法只能算是现在加密算法的雏形,或者仅作为可以借鉴的最初加密思路。
近代密码学
古典密码的安全性受到了威胁,外加使用便利性较低,到了工业化时代,近现代密码被广泛应用。
恩尼格玛机
恩尼格玛机是二战时期纳粹德国使用的加密机器,后被英国破译,参与破译的人员有被称为计算机科学之父、人工智能之父的图灵。

恩尼格玛机使用的加密方式本质上还是移位和替代,只不过因为密码表种类极多,破解难度高,同时加密解密机器化,使用便捷,因而在二战时期得以使用。
恩尼格玛机共有26个字母键和26个带有字母的小灯泡,当按下键盘上的键时,加密后的密文字母所对应的小灯泡就会亮起来,依次记录密文发送给接收者就实现了密文传输。接收者也用相同的恩尼格玛机,依次输入密文并获取原文。
密码机内装有“转子”装置,每按下键盘上的一个字母,“转子”就会自动地转动一个位置,相当于更换了一套密码表。最开始“转子”只有6格,相当于有6套密码表,后来升级到了26格,即有26套密码表。
如果仅仅是26套密码表,和维尼吉亚密码没有安全方面的突出特点,后来恩尼格玛机由一个“转子”升级到了多个“转子”,是密码表套数成指数级增长。例如当有2个“转子”时,密码表套数为26的平方,676种。德国二战期间用的最高水准恩尼格玛机具有8个“转子”,密码表套数为26的8次方,达到了2000多亿种。
恩尼格玛机由6套密码表,升级到676套,甚至到2000多亿套密码表,密码表数量如此之大,在当时靠人工的方法是无法穷尽破解的。看过电影《模仿游戏》的都知道,破解的办法是采用了类似现代计算机的机械机器。
破解像恩尼格玛机这样的机器密码,数学家是至关重要的力量。

20世纪杰出的数学家、现代计算机科学的奠基人–阿兰·图灵
阿兰·图灵
恩尼格玛机的破译一共有两次:
第一次是波兰数学家做出来的,第二次是图灵做出来的。
为什么要破解两次呢?因为这两次使用的恩尼格玛机,结构上不一样。
如果第一次破解难度是65的话,第二次破解难度就要到95了。这还只是难度对比,如果从必要性上对比,第一次破解甚至都是不必要的。
因为波兰情报局在那7年时间里,一直能通过德国间谍搞到每天的秘钥。
情报局只是担心万一今后恩尼格玛机改版,自己没有B方案,所以希望密码学家提前动手。那几年,当那帮密码学家每天埋头破解的时候,情报局高层其实早就提前知道每天的结果了。
可就在二战开打前一年,两个破解渠道一起断掉了:
首先,德国把恩尼格玛机的编码器齿轮增加到了5个,接线板的数量同时也增加了;
其次,那个长期提供当日秘钥的间谍,也突然消失了。
1939年4月,德国撕毁和波兰的互不侵犯条约。所有人都能预见到,德军马上要打来了。波兰坐不住了,赶紧把至今为止其他国家都还不清楚的第一版军用恩尼格玛机的结构、破解方法,公布给了盟友。
英国对波兰提供的方案很重视,甚至为了信息安全扩充了密码队伍。
从从前的密码局40号房换到了布莱切利园(Bletchley Park),面积扩大了几十倍;工作人员从最初的20多人,扩增到五年后的9000多人。
与此同时,员工的结构也有变化。从前主要是语言学家,现在的主力是数学家。大量招募数学家,这是波兰人特地嘱咐英国人的。
英国的资源比波兰丰富得多,所以虽然恩尼格玛机升级过,但靠着堆人力、堆机器的方法,在战争初期,英国竟然可以勉强应付新版恩尼格玛机。
但这时候的破解,可以说是在摸透了人性规律的情况下做出来的,比如:
设定那3个初始值时,按操作规范应该是随机设置,但实际上德军操作员根本做不到这一点。类似QWE、ADS、JKL这样键盘上3个相邻字母的情况,经常出现。操作员就是懒,随手摁出来。
就算3个字母不连着,但手指的活动总是有规律的。3个字母在键盘上的位置总会趋向于集中,所以这些组合总是解码者优先尝试的。
甚至还有用女朋友名字的前三个字母的,以至于后来英国的密码专家每次都先试女人名字。
除此之外,德军的恩尼格玛机操作指南也有漏洞。
比如,5组齿轮中选3组作为当天的编码器,但却有一个规定——不能让同一个齿轮在同一位置连续出现2次。听上去好像是避免了重复,但其实减少了齿轮组合一半的可能性。
还有,接线板对调字母时不能对调相邻的两个字母,比如B不能和A对调,也不能和C对调,理由是这样对调太容易被识别出来。结果这样一规定,可能性的总数又锐减。
所以,英国最初就是利用一切可利用的人性的漏洞、规则的漏洞,外加灵活运用波兰的老方法,勉强支撑着对恩尼格玛机的破译工作。
但这种水平的破译,是远远不够的。一旦德国发现,每条信息的前6位是破译者可以抓住的漏洞的话,就会改变秘钥的传递方式。那样的话英国就没办法了。
所以,图灵的任务就是找到一种全新的破解法,完完全全的猜透恩尼格玛机。
图灵是怎么做的呢?简单说,他也是从一些军事规律导致的漏洞入手的。
比如,德军消息里类似——
无特殊情况(Keine besonderen Ereignisse)
希特勒万岁(Heil Hitler)……
这样的词语,会经常出现。
图灵还分析出了一个更好用的词——“天气”(wetter)。这个词每天早上6点到6:05必然出现,而且大都出现在信息的开头,此外这个词里出现了两个t挨着的情况。
根据我们之前讲过的:
恩尼格玛机对同一个字母连续加密的话,是不会加密成相同字母的,而且这个字母也不会被加密成它本身。
根据这两个规则,图灵就可以拿着 wetter 这个字段当作原文,对照着密文一位一位的挪动,排除掉那些不符合刚刚两个规律的方案。
又因为 wetter 很高概率出现在信息最开头,所以只要试几次,就能发现 wetter 对应的密文到底是哪几个字母。
到了这儿,只是成功的第一步。
因为现在图灵得到的题目就相当于说:已经知道了6个原文和它对应的6个密文,让你求出恩尼格玛机的初始设定。
说这个问题怎么解决呢?
最直接的方法,就是用恩尼格玛机所有的初始设定,一个一个去试。把原文wetter输入,看看密文和我们截获的一样不一样。如果一样,那就说明初始值找对了。
但是,军用版恩尼格玛机的初始值有1.6×10^20那么多种,是不可能用暴力去试的。
所以,可用的方法只有一个——
在手头已有的少量原文和密文之间,想办法建立它们对应的数学关系,来反映出恩尼格玛机的内部结构。
其实这个想法,和波兰破解第一版军用恩尼格玛机有点像。
图灵把原文写一行,密文写在下一行,排成两排,他管这个叫“对照文”(Crib)。然后也建立了环,环上也有连接数的概念。具体细节在这里没法说了,因为非常繁琐,而且和密码学知识的逻辑没太大关系。
我们知道结果就行——图灵通过数学过程的转换,军用版恩尼格玛机1.6×10^20这么多可能性,一下被缩减到了105万种。
可能有人说“这也不少啊”,但这已经是所有可能性的一百万亿分之一了。
这个105万的计算过程,肯定也不能由人来做了,而是用一种机器来破解。这个破解机,就被起名叫“炸弹”。炸弹体积挺大,有2米见方,炸弹机越多破解就越快。

炸弹机(一台)
1940年5月10日,德军也不知是察觉到了什么,突然改变了交换秘钥的方式。每条信息开头的6位,不再是从前的格式了。英国情报部门从此,完全失去了破解德军恩尼格玛机的能力。
好在这个空窗期并不久,3个月后,依照图灵方法制造的第一台炸弹机投入使用。在之后2年里,有50台炸弹机投入使用,英国又能破解德军的密码了。
到1942年的时候,破解德国陆军恩尼格玛机当天的秘钥,大约只需要1小时的时间。
现代密码学
古典加密算法本质上主要考虑的是语言学上模式的改变。直到20世纪中叶,香农发表了《秘密体制的通信理论》一文,标志着加密算法的重心转移往应用数学上的转移。再加上第二次世界大战后计算机与电子学的发展促成了更复杂的密码,而且计算机可以加密任何二进制形式的资料,不再限于书写的文字,以语言学为基础的破密术因此失效。多数计算机加密的特色是在二进制字符串上操作,而不像经典密码学那样直接地作用在传统字母数字上。然而,计算机同时也促进了破密分析的发展,抵消了某些加密法的优势。不过,优良的加密法仍保持领先,通常好的加密法都相当有效率(快速且使用少量资源),而破解它需要许多级数以上的资源,使得破密变得不可行。于是,逐渐衍生出了当今重要的三类加密算法:非对称加密、对称加密以及哈希算法。这三类算法在现实场景中也往往组合起来使用,以发挥最佳效果。
对称加密算法
对称加密算法是使用最广泛的加密算法之一。常用的对称性加密算法有DES算法、AES算法、3DES算法、TDEA算法、Blowfish算法、RC5算法、IDEA算法等。对称加密的特点是,加密和解密两方使用同一密钥进行加、解密。加密算法本身泄露不会对安全性造成影响,密钥才是安全性的关键。按照原理不同,对称加密可以大体分成流加密和分组加密两种类型。
- 流加密
流加密是将明文按字符逐位地,对应地进行加密的一类对称密码算法。流加密中最有名的算法是RC4和GSM。流加密算法相对简单,明文和密钥按位对其做约定的运算,即可获得密文。
最简单的模型是异或流加密例如:

由于流加密原理简单,其算法结构存在弱点,如果密钥流又多次重复使用,只要泄露局部明文,攻击者很容易算出密钥。另外,由于是按位进行加密,攻击者即使对数据进行篡改,也不会破坏原有数据结构,接收者很难发现其中变化。流加密虽然是一种快捷高效的加密方法,但其安全性较低,不建议用户使用流加密对关键信息进行加密。
- 分组加密
分组加密内部实现则复杂的多,每一个加密块都会经历至少16轮运算,其代表算法有DES和AES。目前推荐使用AES,DES已经不在安全。
- DES
DES是较早时期的对称加密标准,在当时得到了广泛的应用。随着计算机性能地不断提高,暴力破解DES变得越来越容易。所以DES已经不再安全,近十几年逐渐地被3DES和AES代替。
DES核心主要分成初始置换、轮函数、逆置换三步。
初始置换:把输入的64位数据块按位重新组合,并把输出分为L0、R0两部分,每部分长32位,其置换规则为将输入的第58位换到第1位,第50位换到第2位……依此类推,最后一位是原来的第7位。L0、R0则是换位输出后的两部分,L0是输出的左32位,R0是右32位,其置换规则见下表:
58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7,
轮函数:DES 使用一个 56 位的密钥以及附加的 8 位奇偶校验位(每组的第8位作为奇偶校验位),产生最大 64 位的分组大小。这是一个迭代的分组密码,使用称为 Feistel 的技术,其中将加密的文本块分成两半。使用子密钥对其中一半应用循环功能,然后将输出与另一半进行“异或”运算;接着交换这两半,这一过程会继续下去,但最后一个循环不交换。
逆置换:DES 使用 16 轮循环,使用异或、置换、代换、移位操作四种基本运算。最后经过16次迭代运算后,得到L16、R16,将此作为输入进行逆置换,逆置换正好是初始置换的逆运算,由此即得到密文输出,解密过程则是整套加密过程的逆运算。
- AES
AES的诞生是为了替代原先的DES,它已经被多方分析论证,在全世界范围广泛使用,是目前最为安全的对称加密算法之一。近十年,AES已然成为对称密钥加密中最流行的算法之一。不同于它的前任标准DES,AES使用的是代换-置换网络,而非Feistel架构。
大多数AES计算是在一个特别的有限域内完成的,加密过程是在一个4×4的字节矩阵上运作,这个矩阵又称为“状态(state)”,其初值就是一个明文区块(矩阵中一个元素大小就是明文区块中的一个Byte)。加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:
- AddRoundKey——矩阵中的每一个字节都与该次轮密钥(round key)做XOR运算;每个子密钥由密钥生成方案产生。
- SubBytes——通过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。
- ShiftRows——将矩阵中的每个横列进行循环式移位。
- MixColumns——为了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每列的四个字节。最后一个加密循环中省略MixColumns步骤,以另一个ddRoundKey取代。
非对称加密算法
对称密码的密钥安全极其重要,加密者和解密者需要提前协商密钥,并各自确保密钥的安全性,一但密钥泄露,即使算法是安全的也无法保障原文信息的私密性。
在实际的使用中,远程的提前协商密钥不容易实现,即使协商好,在远程传输过程中也容易被他人获取,因此非对称密钥此时就凸显出了优势。
非对称密码有两支密钥,公钥(publickey)和私钥(privatekey),加密和解密运算使用的密钥不同。用公钥对原文进行加密后,需要由私钥进行解密;用私钥对原文进行加密后(此时一般称为签名),需要由公钥进行解密(此时一般称为验签)。公钥可以公开的,大家使用公钥对信息进行加密,再发送给私钥的持有者,私钥持有者使用私钥对信息进行解密,获得信息原文。因为私钥只有单一人持有,因此不用担心被他人解密获取信息原文。
私钥对信息的加密(此时一般称为签名),可以确保私钥持有者对信息的认可,大家持有公钥即可验证信息是由私钥持有者发出的,表明私钥持有者认可了信息的内容,实现了对信息进行数字签名的效果。
常见的非对称密码有RSA和SM2。RSA于1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的,三人姓氏开头字母拼成RSA,迄今为止应用十分广泛。SM2基于椭圆曲线公钥密码算法,为我国商用密码体系中用于替换RSA的算法。
非对称密码不仅可以应用于签名、加密中,还可以和对称密码组合形成数字信封,兼顾对称加密技术和非对称加密技术两者的优点,既发挥了对称加密算法速度快的优点,又发挥了非对称加密算法的高安全、无需提前协商的优势。
对称密码算法中加密和解密采用了相同密钥,一但加密者或解密者有一方造成密钥泄露,或在密钥分配传输时泄露,都将对信息安全造成影响。非对称密码算法的提出,解决了这个问题,公钥公开,私钥个人管理,采用非对称密码算法在一定程度上可以简化密钥管理的难题。但由于公钥在分发过程中可能被截取后篡改,接收方也无从核查接收到的公钥所对应私钥的持有者身份,因而非对称密码算法也并不宜大范围使用。
为解决非对称密码算法不宜大范围应用的问题,引入了权威机构CA(certificate authority,数字证书认证机构),由CA负责用户的身份核实,并向用户颁发数字证书,有效地形成公私钥与持有者身份的映射关系,避免了公钥在分发过程中可能被他人偷换的问题,增强了信任性。关于CA、数字证书等相关概念的介绍,将会在后续的文章中详细展开。





